,它不仅关系到数学成绩的提升,更对培养逻辑思维和解决问题的能力具有重要意义,计算技巧的核心在于通过合理的方法简化运算过程,提高计算速度和准确性,从而在面对复杂题目时能够从容应对,以下将从基础巩固、常用技巧、易错点分析和实战应用四个方面展开详细说明。
基础巩固是计算技巧的前提,小学阶段的四则运算、分数、小数、百分数等基础知识必须扎实,20以内的加减法、乘法口诀表要做到脱口而出,这是快速计算的基础,对于分数运算,需要熟练掌握通分、约分的方法,理解分数的基本性质,小数运算中,小数点的移动规则、小数与分数的互化等知识点也不能含糊,建议学生每天进行5-10分钟的基础口算练习,通过听算、视算等方式强化记忆,形成条件反射,熟记一些常用数据,如1-20的平方数、圆周率π的近似值、常见分数与小数的互化结果(如1/2=0.5,1/4=0.25等),能显著提升计算效率。

掌握常用计算技巧是提升能力的关键,这些技巧包括运算定律的灵活运用、巧算与速算方法等,运算定律如加法交换律、结合律,乘法交换律、结合律和分配律,是简化运算的重要工具,计算25×37×4时,可以利用乘法结合律将25×4先计算,得到100,再乘以37,最终结果为3700,这样比直接计算更简便,对于加减法,凑整法是非常实用的技巧,如计算348+297时,可将297拆分为300-3,先算348+300=648,再减去3得到645,分数运算中,裂项法是常用的高级技巧,如计算1/2+1/6+1/12+1/20时,可利用裂项公式1/(n(n+1))=1/n-1/(n+1),将原式转化为(1-1/2)+(1/2-1/3)+(1/3-1/4)+(1/4-1/5),中间项相互抵消,最终结果为1-1/5=4/5,提取公因数、整体代入等方法也能有效简化复杂运算。
易错点分析是避免计算失误的重要环节,学生在计算中常见的错误包括符号错误、运算顺序错误、抄错数字等,符号错误多出现在负数运算中,如-3²与(-3)²的结果完全不同,前者是-9,后者是9,需特别注意运算顺序,运算顺序方面,要牢记“先乘除后加减,有括号先算括号内”的原则,避免因顺序错误导致结果偏差,抄错数字的问题则多由粗心引起,建议学生在计算时养成边算边检查的习惯,或在草稿纸上清晰书写每一步过程,便于核对,分数运算中容易忽略约分的最简形式,小数运算中漏掉小数点的位置也是常见问题,需通过专项练习加以纠正。
实战应用是将计算技巧转化为解题能力的过程,在小升初考试中,计算题往往以混合运算、简便运算、解方程等形式出现,需要学生综合运用多种技巧,计算(3/4+5/6)×12时,可利用分配律展开为3/4×12+5/6×12=9+10=19,避免了通分的繁琐过程,对于解方程,如2(x+3)=10,可通过分配律将方程转化为2x+6=10,再解得x=2,在应用题中,计算技巧同样重要,如涉及百分数的问题,可通过“单位1”的设定简化运算,建议学生通过做真题、模拟题的方式熟悉题型,总结不同题型的解题思路,形成自己的计算策略。
为了更直观地展示常用计算技巧的应用,以下列举几种典型方法的对比: | 常规方法 | 巧算方法 | 结果 | |----------|----------|----------|------| | 125×88 | 125×80+125×8=10000+1000=11000 | 125×(8×11)= (125×8)×11=1000×11=11000 | 11000 | | 7.6×2.5+2.4×2.5 | 7.6×2.5=19,2.4×2.5=6,19+6=25 | (7.6+2.4)×2.5=10×2.5=25 | 25 | | 1/3+1/15+1/35 | 通分计算,公分母为105 | 裂项法:1/(1×3)+1/(3×5)+1/(5×7)= (1/2-1/6)+(1/6-1/10)+(1/10-1/14)=1/2-1/14=3/7 | 3/7 |
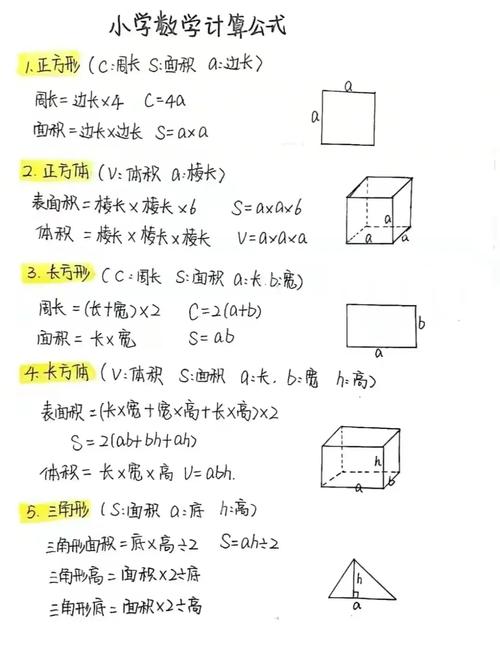
通过对比可以看出,巧算方法能够大幅减少计算步骤,提高效率和准确性。
相关问答FAQs:
问题1:如何提高计算题的准确性,避免粗心出错?
解答:提高计算准确性需要从习惯和方法两方面入手,养成“审题—计算—检查”的完整流程,审题时圈出关键数据和运算符号,计算时草稿纸书写清晰,不跳步,检查时通过逆运算或估算核对结果,建立错题本,记录常犯错误类型(如符号错误、顺序错误),定期复习并针对性练习,每天坚持5-10分钟的限时计算训练,既能提升速度,也能培养专注力,减少粗心概率。
问题2:小升初计算中,分数运算的难点有哪些?如何突破?
解答:分数运算的难点主要在于通分、约分的灵活性以及混合运算的顺序处理,突破方法包括:①理解分数的基本性质,掌握快速找最小公倍数和最大公因数的方法(如短除法);②通过大量练习熟悉分数与小数的互化,根据题目特点选择更简便的形式;③对于复杂分数运算,学会整体观察,合理运用运算定律(如分配律)简化计算,例如将(1/2+1/3)×6转化为1/2×6+1/3×6=3+2=5,注意运算顺序,避免因急于求成而忽略括号或优先级规则。