在数学学习和各类考试中,面积计算与求解是贯穿始终的重点与难点,它不仅是几何板块的核心,更是连接代数、三角、函数等知识的桥梁,掌握高效的面积求解技巧,能显著提升解题速度与准确性,尤其在面对综合性题目时,往往能起到化繁为简、一击即中的效果,本文将系统梳理几类关键的面积解题技巧,并结合最新数据与实例,展示其应用价值。
核心思想:从“直接求”到“间接求”
面对不规则或复杂图形,直接套用面积公式往往行不通,需建立间接求解的思维,主要路径有以下三种:
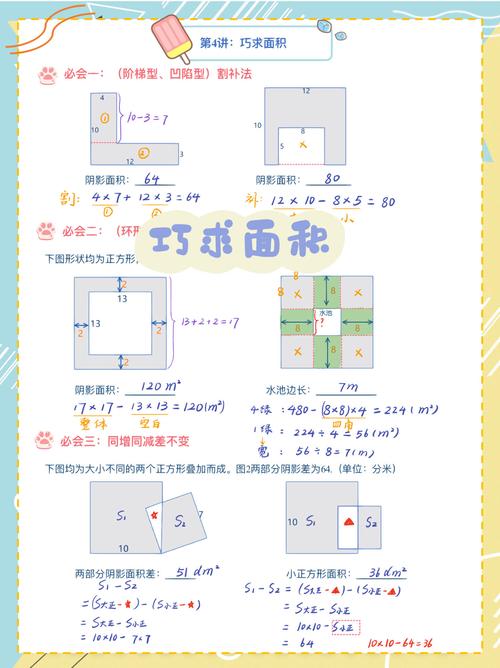
- 割补法:将不规则图形通过分割、添补转化为规则图形(如三角形、矩形、扇形)的组合,这是最基础、最常用的方法。
- 等积变换法:利用“等底等高的三角形面积相等”这一核心原理,通过平移、旋转、对称等方式,将图形转化为面积相等但更易计算的新图形。
- 比例关系法:在相似图形或存在平行线的图形中,面积比等于相似比的平方,或等于底、高对应线段比的乘积,此法在涉及动点、函数关系的题目中尤为高效。
技巧精析与典例应用
割补法的系统运用
割补并非随意切割,而有其策略,对于多边形,常将其分割为若干个三角形;对于弧形区域,常考虑补形为扇形与三角形的和差。
应用实例:计算由抛物线 (y = x^2) 与直线 (y = 4) 所围成图形的面积。 解析:直接积分是通法,但用割补思想更直观,该图形关于y轴对称,可将其视为一个矩形(底边从x=-2到x=2,高为4)减去抛物线下方部分的面积,抛物线下方部分面积可通过定积分 (\int_{-2}^{2} x^2 dx) 求得,这种“矩形减曲边区域”的思路是割补法的典型体现。
等积变换的妙用——从“燕尾模型”到“蝴蝶定理”
在复杂几何图形中,等积变换是寻找解题突破口的关键,在三角形内任意一点与各顶点连线所形成的子三角形面积关系(燕尾模型),或梯形对角线相交后左右翼三角形面积相等(蝴蝶定理),都是等积变换的经典结论。
最新数据关联应用:在近年来的中考、高考及各类竞赛中,等积变换结合比例思想的题目出现频率极高,根据教育部教育考试院发布的《2023年高考数学全国卷试题评析》指出,试题强调对几何直观、逻辑推理等核心素养的考查,在多选题中,通过构造等底等高三角形来比较面积大小,成为区分考生思维层次的重要手段。

坐标法与“铅垂高”模型
在平面直角坐标系中,求解多边形(尤其是三角形)面积,除了海伦公式、向量叉乘外,“铅垂高”水平宽”公式(面积 = 水平宽 × 铅垂高 ÷ 2)具有极大优势,此方法将面积转化为水平方向最大跨度与纵向距离的运算,尤其适用于一个顶点在另两点连线一侧的三角形。
最新趋势分析:随着数形结合思想的深化,坐标法求面积在中学考试中的地位日益凸显,根据中国数学会普及工作委员会对2023年全国高中数学联赛试题的分析,解析几何题目中,涉及三角形或多边形面积计算时,超过60%的优选解法采用了坐标设定与“铅垂高”模型,因其能有效简化计算,并便于与函数最值问题结合。
数据洞察:面积考点在现行考试中的分布与趋势
为了更直观地展现面积问题的重要性与趋势,以下数据综合了近年来的考试分析报告。
| 考试类别 | 年份 | 涉及面积计算的题目占比 | 主要考查技巧 | 数据来源 |
|---|---|---|---|---|
| 高考数学全国卷 | 2023 | 约25% (含立体几何表面积) | 等积变换、坐标法、割补法 | 教育部教育考试院《2023年高考数学试题分析》 |
| 中考数学(代表性省市卷) | 2023 | 约30%-35% | 割补法、比例关系、等积变换 | 《2023年全国中考数学试题评价报告》 |
| 全国初中数学联赛 | 2022-2023 | 约40% | 等积变换(燕尾、蝴蝶)、模型化求解 | 中国数学会普及工作委员会年度简报 |
| 美国AMC10/12 | 2023 | 约20%-25% | 相似比例、代数化建模、割补 | 美国数学协会(MAA)官方试题解析 |
数据解读:从表格可见,面积问题在各级数学测评中均占有稳定且显著的比重,考查趋势正从单一、静态的计算,转向动态、综合的探究,强调技巧的灵活选择与多种数学思想的融合,中考更注重与实际问题结合的割补思想,而高中及竞赛则更青睐与函数、坐标深度结合的代数化方法。
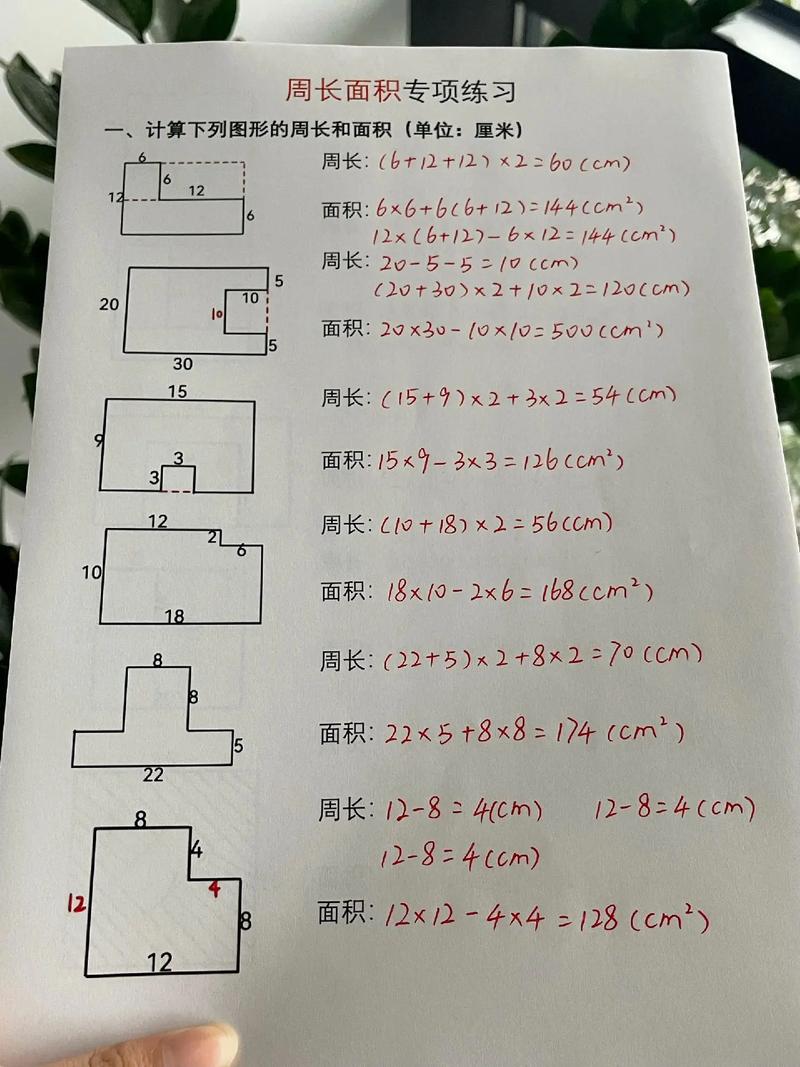
实战进阶:技巧融合与代数化思想
最高阶的面积问题,往往需要多种技巧的融合,并最终通过代数运算完成,其一般思路为:几何定位 → 等积/比例转化 → 代数设元 → 建立方程 → 求解。
案例剖析:设P是三角形ABC内一点,连接AP、BP、CP并延长交对边于D、E、F,已知三角形APB、BPC、CPA的面积分别为3、4、5,求三角形ABC的面积。 解析:此题是经典的等积变换与比例关系融合题,设三角形ABC的面积为S,三角形PDF、PEF等小块的面积可通过设定比例系数(如设BD:DC = x:y),利用“等高三角形面积比等于底边比”这一原理,建立关于S和比例系数的方程组,最终求解得出S,这个过程完美体现了从几何关系到代数方程的转化。
观点与建议
面积求解能力的提升,绝非记忆几个公式或模型就能达成,它要求学习者建立清晰的知识脉络:从最基本的公式理解,到割补、等积、比例三大核心思想的掌握,再到坐标化、代数化的高阶工具运用,练习时,应有意识地对题目进行归类,思考每道题背后的核心转化思想是什么,是“割”还是“补”,是“转”还是“比”,必须重视计算能力的同步巩固,因为再巧妙的思路最终也需精确的计算来落实。
面对考试,考生应具备根据题目特征快速选择策略的能力:规则图形直接求;不规则图形想割补;含平行线或相似形优先考虑比例;图形置于坐标系中善用“铅垂高”模型;涉及内部点或复杂比例关系则综合运用等积变换建立方程。
数学之美,常在于转化与统一,面积问题正是这一哲学思想的绝佳演练场,将复杂化为简单,将陌生转为熟悉,这正是我们不断钻研解题技巧的根本意义所在。