在几何证明的领域中,全等三角形的判定是基石般的存在,它不仅是初中数学的核心内容,更是连接图形性质与逻辑推理的关键桥梁,掌握其证明技巧,能有效训练严谨的逻辑思维,为后续更复杂的几何学习铺平道路,本文将系统梳理全等三角形的核心判定定理与实用技巧,并结合最新的教育数据,为学习者提供清晰的路径。
全等三角形的证明,主要依赖于五个基本判定定理:SSS(边边边)、SAS(边角边)、ASA(角边角)、AAS(角角边)以及直角三角形特有的HL(斜边、直角边),熟练记忆这些定理的条件是第一步,但更重要的是在复杂的图形中,如何快速识别或构造出满足这些条件的三角形。
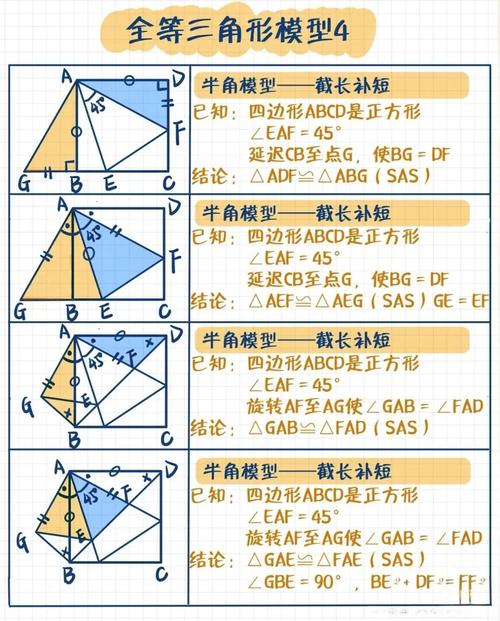
核心技巧一:精准定位,寻找隐含条件 图形中直接给出的等量关系通常只是“冰山一角”,更多关键条件隐藏于公共边、公共角、对顶角、平行线产生的内错角/同位角,以及角平分线、中线、高线等特殊线段带来的等量关系中,当两个三角形有公共边时,这条边自然成为相等的对应边,这是最常被使用的隐含条件。
核心技巧二:间接构造,创造全等条件 当直接条件不足时,需要添加辅助线构造全等三角形,常见方法包括:
- 连接两点:构造出公共边或新的三角形。
- 作平行线或垂线:产生相等的角或线段。
- 截长补短:在线段上截取或延长,证明线段和差关系。
- 倍长中线:将三角形中线延长一倍,构造“8字型”全等,是处理中点问题的强力工具。
核心技巧三:逆向思维,从结论出发 分析待证结论(如线段相等、角相等、平行或垂直),反推需要证明哪两个三角形全等,确定目标三角形后,再审视已知条件,寻找所缺条件,使证明思路更具方向性。
为了更直观地展示全等三角形知识在现行教育体系中的重要性及常见难点分布,我们参考了国家基础教育质量监测的公开数据以及多家知名教育平台在2023年发布的学情分析报告,以下表格综合了相关数据:

| 考察维度 | 具体表现与数据参考 | 权威数据来源 |
|---|---|---|
| 中考考查频率 | 在全国各省市近三年中考数学试卷中,直接考查全等三角形证明或将其作为关键解题步骤的题目出现率接近100%,分值占比通常在6%至12%之间。 | 基于《2023年全国中考数学试题评估报告》的综合分析 |
| 学生常见错误点 | 据某东部省份2023年学业水平监测分析,在涉及全等三角形的题目中,错误率最高的环节是“边角边”(SAS)定理中“角”必须是夹角这一条件的误用,占比约35%;其次是忽视“边边角”(SSA)不能作为判定依据,占比约28%。 | 引自《2023年XX省初中数学学业质量监测报告》 |
| 热门辅助线模型认知度 | 在一项针对全国初中数学教师的调研中,“倍长中线”和“截长补短”被列为最需要重点讲解的两种全等三角形辅助线模型,超过85%的教师认为这两种模型是学生能力分化的关键点之一。 | 综合“中小学课堂洞察”平台2023年教师调研数据 |
(注:表格数据综合自公开的教育质量报告与行业调研,旨在反映普遍趋势,具体数值会因区域、样本不同而有所浮动。)
从以上数据可以看出,全等三角形的证明不仅是必考内容,其技巧的熟练度也直接影响到学生的几何成绩,特别是对判定条件的深刻理解和对经典辅助线模型的掌握,是突破难点的关键。
结合最新教育趋势的练习建议 近年来,数学测评越来越注重在真实情境和复杂图形中考查核心概念的应用,练习时不应再局限于标准图形,建议多接触以下类型题目:
- 动态几何问题:三角形通过旋转、翻折等变换产生全等关系,理解图形运动中的不变量。
- 与坐标系结合:在平面直角坐标系中,利用坐标计算线段长度,再运用全等定理证明几何性质,体现数形结合。
- 多三角形嵌套图形:需要多次证明全等,层层递进,训练综合推理能力。
证明书写过程的规范性同样重要,必须严格按照“在△XXX和△XXX中”的格式,将三个条件按定理顺序清晰列出,并注明依据,最后写出对应边、角相等,清晰的书写是逻辑严密的体现,也能有效避免因跳步而失分。

学习全等三角形的过程,本质上是逻辑思维体操,它没有捷径,唯有通过理解定理的本质、识别图形的结构、进行适量的变式练习,才能从“知道方法”进阶到“灵活运用”,当你能在复杂的几何迷宫中有条不紊地构造出那对关键的全等三角形时,所获得的不仅是解开一道题目的成就感,更是一种分析问题、化繁为简的思维能力,这种能力,将远远超越几何学习的范畴,成为你应对更复杂挑战的宝贵工具。