开平方是数学运算中常见的一种操作,尤其在解决几何问题、物理计算或工程测量时经常需要用到,对于一些简单的完全平方数,如4、9、16等,开平方可以直接得出整数结果;但对于非完全平方数或较大的数字,手动开平方可能会显得复杂,掌握一些技巧可以大大简化开平方的过程,提高计算效率和准确性,本文将详细介绍几种实用的开平方技巧,帮助读者快速掌握这一运算方法。
我们需要了解开平方的基本概念,开平方是指求一个非负实数的平方根的运算,记作√x。√9=3,因为3²=9,对于非完全平方数,如√10,结果是一个无限不循环小数,通常需要保留一定的小数位数,手动开平方时,可以通过逐步逼近的方法找到近似值,而一些技巧则能让我们更高效地完成这一过程。
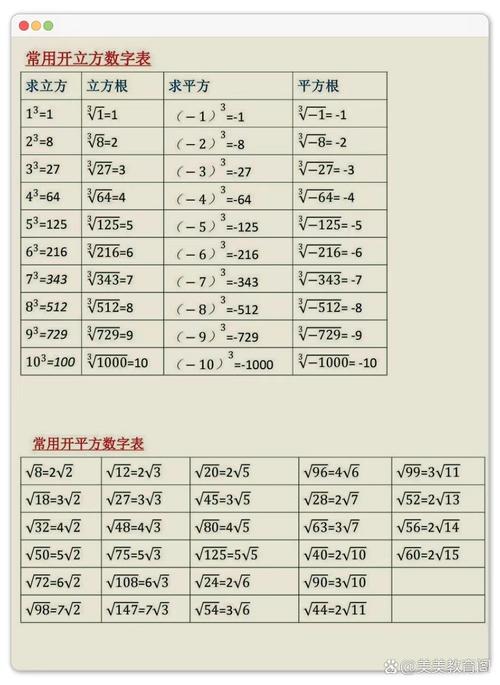
第一种技巧是“因式分解法”,这种方法适用于可以分解为完全平方数的乘积的数字,计算√72时,可以先将72分解为36×2,其中36是完全平方数(6²),72=√(36×2)=6√2,这种方法的关键在于快速识别数字中的完全平方因数,常见的完全平方数有1、4、9、16、25、36、49、64、81、100等,熟悉这些数可以大大提高分解效率,对于较大的数字,可以先尝试除以较大的完全平方数,逐步简化计算。
第二种技巧是“估算法”,适用于无法快速分解的非完全平方数,计算√10时,我们知道3²=9,4²=16,10介于3和4之间,为了更精确地估算,可以取3.1²=9.61,3.2²=10.24,发现3.1²更接近10,10≈3.1,如果需要更高精度,可以继续计算3.16²=9.9856,3.17²=10.0489,10≈3.16,这种方法的优点是直观易懂,适合快速估算,但缺点是精度有限,需要多次尝试才能达到理想结果。
第三种技巧是“长除法”,这是一种更系统化的手动开平方方法,适用于任意数字,且可以精确到任意小数位,以计算√5为例,具体步骤如下:将5从小数点开始向每两位一组分段,即5.00 00 00;找出最大的整数a,使得a²≤5,这里a=2(因为2²=4),将2写在商的位置,4写在5下方,相减得1;将下一段的00移下来,得到100,然后将当前的商(2)乘以20,得到40,再找一个数字b,使得(40+b)×b≤100,这里b=2(因为42×2=84),将2写在商的下一位置,84写在100下方,相减得16;再将下一段的00移下来,得到1600,将当前的商(22)乘以20,得到440,找一个数字c,使得(440+c)×c≤1600,这里c=3(因为443×3=1329),将3写在商的下一位置,1329写在1600下方,相减得271,重复这一过程,可以得到√5≈2.233,长除法虽然步骤较多,但逻辑清晰,适合需要高精度计算的情况。
第四种技巧是“牛顿迭代法”,这是一种数值逼近方法,收敛速度快,适合编程计算或需要高精度的情况,牛顿迭代法的公式为:xₙ₊₁ = (xₙ + S/xₙ)/2,其中S是要求平方根的数字,xₙ是当前的近似值,计算√10时,可以取初始值x₀=3,然后计算x₁=(3+10/3)/2≈3.1667,x₂=(3.1667+10/3.1667)/2≈3.1623,x₃≈3.16228,已经非常接近√10的精确值,牛顿迭代法的优点是收敛速度快,通常只需几次迭代就能达到很高的精度,但需要一定的数学基础。

第五种技巧是“利用平方表或计算器”,这是最直接的方法,适合日常计算,平方表列出了常见数字的平方根,可以直接查找;计算器则能快速给出精确结果,虽然这种方法不涉及手动计算的技巧,但在实际应用中非常高效,尤其是在处理复杂数字时。
为了更直观地比较不同方法的适用场景,以下表格总结了上述技巧的特点:
| 方法 | 适用场景 | 优点 | 缺点 |
|---|---|---|---|
| 因式分解法 | 可分解为完全平方数的数字 | 计算简单,结果精确 | 仅适用于特定数字 |
| 估算法 | 快速估算非完全平方数 | 直观易懂,速度快 | 精度有限,需多次尝试 |
| 长除法 | 需要高精度的任意数字 | 系统化,可精确到任意位 | 步骤较多,耗时 |
| 牛顿迭代法 | 需要高精度的编程或科学计算 | 收敛速度快,精度高 | 需要数学基础,初始值影响大 |
| 平方表/计算器 | 日常快速计算 | 高效,结果精确 | 依赖工具,不锻炼计算能力 |
在实际应用中,可以根据具体需求选择合适的方法,在考试中,如果时间紧张且数字简单,可以优先使用因式分解法或估算法;如果需要高精度结果,则可以选择长除法或牛顿迭代法,对于日常生活中的快速计算,使用计算器则是最便捷的选择。
需要注意的是,开平方运算中还有一些常见错误需要避免,混淆平方根和算术平方根的概念(算术平方根是非负的),或者在长除法中分段错误(必须从整数部分开始,每两位一组),对于负数的开平方,在实数范围内是没有意义的,只有在复数范围内才能进行运算。

相关问答FAQs:
-
问:如何快速判断一个数字是否为完全平方数?
答:可以通过观察数字的个位数来判断,完全平方数的个位数字只能是0、1、4、5、6或9,数字121的个位数是1,可能是完全平方数(实际为11²);而数字123的个位数是3,不可能是完全平方数,还可以通过计算数字的平方根是否为整数来判断,100=10,是整数,因此100是完全平方数。 -
问:开平方时如何选择合适的小数位数?
答:小数位数的选择取决于实际需求,在工程测量中,可能需要保留2-3位小数;而在科学计算中,可能需要更高的精度,可以通过逐步计算并比较相邻两位的差值来判断是否达到足够的精度,计算√2时,如果3.141²≈9.865,3.142²≈9.872,而实际需要精度到小数点后两位,则可以取3.14作为近似值。











