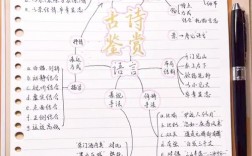
,掌握这些技巧不仅能快速解决整除相关的题目,还能培养逻辑思维和数感,整除问题的核心在于利用数字的构造特征、运算性质以及特定规律,通过灵活的方法判断一个数是否能被另一个数整除,以下从基础技巧、进阶方法、实战应用三个方面展开详细说明。
基础技巧中,最常用的是“数字和法”和“末位判断法”,数字和法适用于判断被3或9整除的情况:一个数能被3(或9)整除,当且仅当其各位数字之和能被3(或9)整除,例如判断12345是否能被3整除,其数字和为1+2+3+4+5=15,15能被3整除,因此12345能被3整除,末位判断法则主要用于判断被2、5、10整除的情况:末位是偶数(0、2、4、6、8)的数能被2整除,末位是0或5的数能被5整除,末位是0的数能被10整除,被4或25整除的判断只需看末两位数字,因为100是4和25的倍数;被8或125整除则需看末三位数字,因为1000是8和125的倍数,这些方法基于十进制数的位值原理,通过局部数字的特征快速得出结论。

进阶技巧包括“差值法”和“分解因数法”,差值法适用于判断被11整除的情况:一个数能被11整除,当且仅当其奇数位数字之和与偶数位数字之和的差能被11整除(差为0或11的倍数),例如判断121是否能被11整除,奇数位数字和为1+1=2,偶数位数字和为2,差为0,因此121能被11整除,分解因数法则是将除数分解为互质的因数,分别判断整除性,例如判断被6整除,需同时满足被2和被3整除;被12整除则需同时满足被3和被4整除,这种方法的关键在于利用“若一个数能被a和b整除,且a与b互质,则能被a×b整除”的性质。
实战应用中,往往需要结合多种技巧,例如解决“一个七位数9□2□3□5能被72整除,方框内应填什么数字?”这类问题时,首先分解72=8×9,且8与9互质,根据被8整除的规则,末三位35□需能被8整除,通过尝试可知352÷8=44,因此末位填2;再根据被9整除的规则,各位数字之和9+□+2+□+3+2+5=21+2□需能被9整除,21+2□=27或36,解得□=3或7.5(舍去),因此千位填3,最终数字为9323252,验证其能被72整除。
为更直观展示常见除数的判断规则,可总结如下表:
| 除数 | 判断规则 | 示例(判断123456) |
|---|---|---|
| 2 | 末位是偶数 | 6是偶数,能被2整除 |
| 3 | 数字和能被3整除 | 1+2+3+4+5+6=21,21÷3=7,能整除 |
| 4 | 末两位数能被4整除 | 56÷4=14,能整除 |
| 5 | 末位是0或5 | 末位6,不能整除 |
| 8 | 末三位数能被8整除 | 456÷8=57,能整除 |
| 9 | 数字和能被9整除 | 21不能被9整除,不能整除 |
| 11 | 奇数位和与偶数位和的差能被11整除 | (1+3+5)-(2+4+6)=9-12=-3,不能整除 |
相关问答FAQs:
-
问:如何快速判断一个数是否能被7整除?
答:判断被7整除可采用“截尾倍减法”:将数的末位数字截去,用剩余部分减去末位数字的2倍,重复此过程直至得到较小数,若结果能被7整除,则原数能被7整除,例如判断343:截去末位3,剩余34减去3×2=6,得28,28÷7=4,因此343能被7整除。 -
问:在复杂整除问题中,如何避免遗漏条件?
答:可采用“分步验证法”:首先分解除数的因数(如72分解为8×9),再逐一验证每个因数的整除条件,最后综合结果,将条件转化为方程或不等式(如数字和满足特定关系),通过枚举或代数方法求解未知数,确保所有条件同时满足。