核心思维理念:从“算”到“想”
在开始具体技巧前,家长和孩子首先要建立正确的观念:
- 奥数 ≠ 偏题、怪题:奥数题目是课本知识的延伸和拓展,它考察的是对数学概念的理解深度和灵活运用能力。
- 过程比答案更重要:一道题不会做,没关系,关键是让孩子思考:“我卡在哪里了?”“为什么这个方法不行?”“有没有别的角度可以切入?” 这种思考过程本身就是最大的收获。
- 培养“数感”和“图形感”:对数字的敏感(如快速发现倍数关系、奇偶性)和对图形的直观感受(如看到对称、旋转、平移)是解决很多奥数题的基础。
通用解题技巧(“万能钥匙”)
这些技巧适用于几乎所有奥数题型,是解题的底层逻辑。
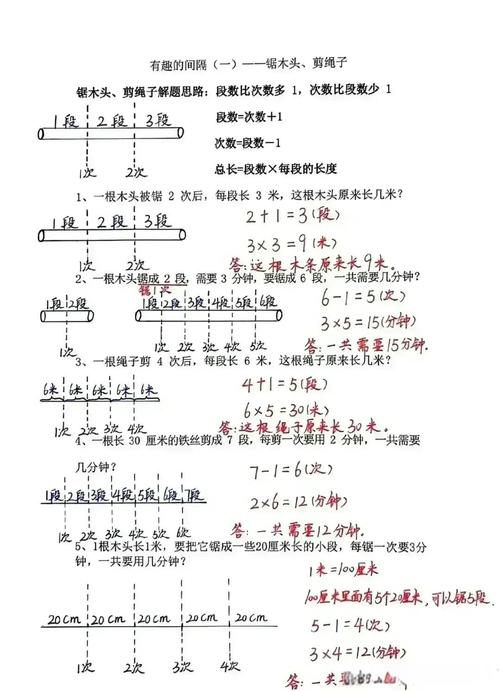
画图法
这是最重要、最直观的技巧,没有之一,尤其适用于应用题、几何题和行程问题。
- 线段图:专门用于解决和差、和倍、差倍问题,以及复杂的行程问题(如相遇、追及),通过画线段,可以清晰地展示各个量之间的关系。
- 示意图:用于解决植树问题、方阵问题、年龄问题等,用简单的图形或符号代替实物,帮助理解题意。
- 几何图:用于解决几何问题,一定要养成规范作图的习惯,标出已知条件,辅助线要清晰。
【例】:哥哥和妹妹共有20本书,哥哥比妹妹多4本,两人各有多少本?
- 画线段图:画两条线段,一条代表哥哥,一条代表妹妹,哥哥的线段比妹妹的长一小段,标上“4”,两条线段的总和是“20”。
- 观察:从总和20中减去多的4本,剩下的16本就是妹妹的两倍,所以妹妹有8本,哥哥有12本。
列举法(枚举法)中的数量范围不大时,把所有可能的情况一一列出来,是简单有效的方法。
- 有序列举:为了避免重复和遗漏,一定要按照一定的顺序(如从小到大)来列举。
- 分类列举:当情况较多时,可以分成不同类别来列举。
【例】:用1、3、5三个数字可以组成多少个不同的三位数?(每个数字只用一次)
- 有序列举:
- 百位是1,十位是3,个位是5 -> 135
- 百位是1,十位是5,个位是3 -> 153
- 百位是3,十位是1,个位是5 -> 315
- ... (以此类推)
- 一共可以组成6个不同的三位数。
假设法中出现“....”或者关系复杂时,可以做一个大胆的假设,然后根据假设与实际情况的差异进行调整。
【例】:鸡兔同笼,共10个头,28条腿,问鸡和兔各有多少只?

- 假设:假设笼子里全是鸡,那么应该有 10 × 2 = 20 条腿。
- 比较:实际上有28条腿,比假设多了 28 - 20 = 8 条腿。
- 调整:为什么会多?因为我们把每只兔子都当成了鸡,每只兔子少算了 4 - 2 = 2 条腿,多出来的8条腿,意味着有 8 ÷ 2 = 4 只兔子。
- 兔子有4只,鸡有 10 - 4 = 6 只。
转化法
把一种问题形式转化为另一种更熟悉或更简单的问题形式。
- 单位“1”的转化:在分数应用题中,关键是找到单位“1”,并灵活地进行转化。
- 问题转化:把求甲的问题,转化为先求乙,再通过乙求出甲。
【例】:一项工程,甲队单独做10天完成,乙队单独做15天完成,两队合作,几天完成?
- 转化:把“工程总量”看作单位“1”。
- 甲队的工作效率是 1/10(每天完成工程的十分之一)。
- 乙队的工作效率是 1/15。
- 两队合作的工作效率是 (1/10 + 1/15) = 1/6。
- 所需时间 = 总工作量 ÷ 工作效率 = 1 ÷ (1/6) = 6 天。
逆推法(倒推法)
从问题的最后结果出发,一步一步倒着往前推算,适用于还原问题。
【例】:一个数,加上3,乘以3,减去3,除以3,最后等于3,这个数原来是多少?
- 倒推:
- 3,是“除以3”得到的,所以之前是 3 × 3 = 9。
- 9是“减去3”得到的,所以之前是 9 + 3 = 12。
- 12是“乘以3”得到的,所以之前是 12 ÷ 3 = 4。
- 4是“加上3”得到的,所以原来的数是 4 - 3 = 1。
- 这个数原来是1。
专题常用方法
针对不同专题,有一些更“专用”的技巧。
| 专题 | 核心技巧 | 简要说明 |
|---|---|---|
| 计算巧算 | 运算定律、凑整法、裂项法、换元法 | 灵活运用加法/乘法交换律、结合律、分配律,通过分组、拆分、抵消来简化计算。 |
| 应用题 | 画图法、假设法、方程思想(高年级) | 线段图是灵魂,学会找等量关系,将文字语言转化为数学语言。 |
| 行程问题 | 画线段图、公式法(S=VT)、比例法 | 核心是速度、时间、路程三者关系,相遇、追及问题模型要熟练。 |
| 数论问题 | 奇偶性分析、整除特征、余数问题、枚举法 | 掌握2,3,4,5,8,9,11等数的整除特征,利用奇偶性进行排除。 |
| 几何问题 | 等积变形、割补法、公式法、对称法 | 面积、周长、体积公式要记牢,通过平移、旋转、割补,将不规则图形转化为规则图形。 |
| 计数问题 | 加法原理、乘法原理、容斥原理、捆绑法、插空法 | 分类用加法,分步用乘法,注意不重不漏,排列组合的入门技巧。 |
| 组合数学 | 抽屉原理、最不利原则 | 解决“至少”、“保证”类问题,关键在于构造“抽屉”。 |
| 逻辑推理 | 列表法、排除法、假设法 | 用表格或列表整理信息,根据条件进行肯定和否定,逐步缩小范围。 |
学习与训练建议
- 精选习题,拒绝题海:做一道题就要有一道题的收获,选择经典的、有代表性的题目,吃透它,做完后要反思:这道题考的是什么?用了什么方法?有没有别的解法?
- 建立错题本:这是提分的关键!不仅要抄错题,更要写下错误原因(是概念不清?计算失误?还是思路错误?)和正确思路,定期回顾错题本,避免重复犯错。
- 一题多解,多题一解:
- 一题多解:尝试用不同的方法解决同一道题,可以拓宽思路,比较不同方法的优劣。
- 多题一解:做完一类题后,总结它们的共同点,找到背后的通用模型或解题思路,做到举一反三。
- 鼓励孩子讲题:当孩子做出一道题后,让他/她尝试把解题思路讲给家长或同学听,能讲清楚,才说明真正理解了,这是检验学习效果的最好方式。
- 保持兴趣,循序渐进:奥数学习是一个长期过程,切忌急功近利,遇到难题很正常,要鼓励孩子,培养他克服困难的勇气和信心,可以从简单的趣味数学入手,逐步过渡到系统的奥数学习。
总结一下:小学奥数解题的精髓在于“转化”和“建模”,将复杂问题转化为简单问题,将具体问题抽象成数学模型,而这一切都建立在扎实的计算基础和强大的逻辑思维能力之上,希望这些技巧和建议能对您和孩子有所帮助!